Intro to Computer programming worked at calculating digits of pi today. The actual algorithms aren’t too bad, but getting more than the standard number of digits from a double is a bit trickier. Here’s a program that calculates pi using:

Bailey–Borwein–Plouffe formula

Bellard’s formula

and
Chudnovsky algorithm

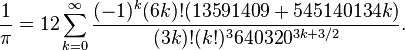
Holy smokes is Chudnovsky algorithm’s fast!

            Plouff          Bellard             Chudnovsky
Iteration number  1   3.133333333333333333333333   3.141765873015873015873017   3.141592653589734207668453
Iteration number  2   3.141422466422466422466422   3.141592571868390306374053   3.141592653589793238462642
Iteration number  3   3.141587390346581523052111   3.141592653642050769944284   3.141592653589793238462642
Iteration number  4   3.141592457567435381837004   3.141592653589755368080514   3.141592653589793238462642
Iteration number  5   3.141592645460336319557021   3.141592653589793267843377   3.141592653589793238462642
Iteration number  6   3.141592653228087534734378   3.141592653589793238438852   3.141592653589793238462642
Iteration number  7   3.141592653572880827785241   3.141592653589793238462664   3.141592653589793238462642
Iteration number  8   3.141592653588972704940778   3.141592653589793238462644   3.141592653589793238462642
Iteration number  9   3.141592653589752275236178   3.141592653589793238462644   3.141592653589793238462642
Iteration number  10   3.141592653589791146388777   3.141592653589793238462644   3.141592653589793238462642
Iteration number  11   3.141592653589793129614171   3.141592653589793238462644   3.141592653589793238462642
Iteration number  12   3.141592653589793232711293   3.141592653589793238462644   3.141592653589793238462642
Iteration number  13   3.141592653589793238154767   3.141592653589793238462644   3.141592653589793238462642
Iteration number  14   3.141592653589793238445978   3.141592653589793238462644   3.141592653589793238462642
Iteration number  15   3.141592653589793238461733   3.141592653589793238462644   3.141592653589793238462642
Iteration number  16   3.141592653589793238462594   3.141592653589793238462644   3.141592653589793238462642
Iteration number  17   3.141592653589793238462641   3.141592653589793238462644   3.141592653589793238462642
Iteration number  18   3.141592653589793238462644   3.141592653589793238462644   3.141592653589793238462642
Iteration number  19   3.141592653589793238462644   3.141592653589793238462644   3.141592653589793238462642

Source code (Python)

from decimal import *

#Sets decimal to 25 digits of precision
getcontext().prec = 25

def factorial(n):
    if n<1:
        return 1
    else:
        return n * factorial(n-1)

def plouffBig(n): #http://en.wikipedia.org/wiki/Bailey%E2%80%93Borwein%E2%80%93Plouffe_formula
    pi = Decimal(0)
    k = 0
    while k < n:
        pi += (Decimal(1)/(16**k))*((Decimal(4)/(8*k+1))-(Decimal(2)/(8*k+4))-(Decimal(1)/(8*k+5))-(Decimal(1)/(8*k+6)))
        k += 1
    return pi

def bellardBig(n): #http://en.wikipedia.org/wiki/Bellard%27s_formula
    pi = Decimal(0)
    k = 0
    while k < n:
        pi += (Decimal(-1)**k/(1024**k))*( Decimal(256)/(10*k+1) + Decimal(1)/(10*k+9) - Decimal(64)/(10*k+3) - Decimal(32)/(4*k+1) - Decimal(4)/(10*k+5) - Decimal(4)/(10*k+7) -Decimal(1)/(4*k+3))
        k += 1
    pi = pi * 1/(2**6)
    return pi

def chudnovskyBig(n): #http://en.wikipedia.org/wiki/Chudnovsky_algorithm
    pi = Decimal(0)
    k = 0
    while k < n:
        pi += (Decimal(-1)**k)*(Decimal(factorial(6*k))/((factorial(k)**3)*(factorial(3*k)))* (13591409+545140134*k)/(640320**(3*k)))
        k += 1
    pi = pi * Decimal(10005).sqrt()/4270934400
    pi = pi**(-1)
    return pi
print "\t\t\t Plouff \t\t Bellard \t\t\t Chudnovsky"
for i in xrange(1,20):
    print "Iteration number ",i, " ", plouffBig(i), " " , bellardBig(i)," ", chudnovskyBig(i)

Next Post Previous Post