So this summer I have some curriculum days to spend at school, and as a break from creating a “21st century” project for Applied Math, I’m going through the course evaluation that my Geometry kids took on the last day of class. BTW, google forms totally rock for this. You quickly put together a list of questions (free response short or long, multiple choice, etc), and then you get a link to share. When the form gets filled in, the data gets put into a spreadsheet and you’re all set. Pretty neat stuff. Here is a pdf of feedback form: geometry course eval.

Anywho, this was the first time I’ve given a course evaluation (thanks to Matt for his template), and it was a little nerve wracking. Not because I think I’m a horrible teacher and the kids would ream into me, but because I wasn’t sure what to do with the feedback. Sort of a fear of a vacuum thing.

First topic under the gun:

Homework

On the whole the geometry students found the homework to be easy-ish and fairly graded. I graded only on completion (4pts compete, 2pts half done), and if it wasn’t done they had a chance to bring it in next class for half-credit. The vast majority of students didn’t take advantage of this, but the ones who did were grateful. There were many comments about how in the long run homework helped, and when they slipped up on homework they slipped up on tests and quizzes. I plan on using this student support for homework (!) on future classes, maybe they’ll listen a bit more when it comes from different sources.

In the long run I plan to greatly reduce the amount of points and time that homework consumes, but philosophically I feel I need to phase that in slowly with the students (Cornally-Hulk angry?) .

What did we do too much of?

I submit a wordle cloud to explain their responses: Is that clear then? We need (?) to spend about 18% of our time on proofs in our Geometry Regents class, so that our state can weigh proofs at about 6% of the final exam (</whining>). Not to mention that our time with proofs doesn’t get many of them very far at all. Its a frustrating topic for a lot of kids and man are they “squeaky wheels” about not getting it. The cool thing is that the quarter of the kids that do “get it” are not typically they kids who did well in previous algebra and geometry topics… I like that.

What did we do too little of?

Alright wordle time again:Well Mr. Holmes what do you make of that? Now we did too little proofs? I think it boils down to a matter of preference, some feel like we spent too much time on Proofs because they didn’t get them, and some feel like we spent too little time on Proofs because they didn’t get them.

Interestingly enough the two topics we finished with, circles and constructions, were big too. Is that just a bias about what topics they know we did and what immediately came to mind when they filled out the form?

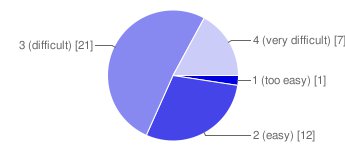
Overall I found this exercise to be interesting, but the muddy results screw with my logical brain. I want the results to be clear and obvious but naturally that is not going to be the case. I might get where to buy generic cialis UK more concrete answers when we get back the item analysis for our exam. I will definitely do this next year, with more one-word answers or multiple choice. The comments are great to read, but difficult to parse. I’ll finish up with a pie chart (created by google) for the difficulty of this course… I think it looks good, but who knows?

p.s. Clearly my students have awful spelling! Oh well, I’m no english teacher 😉