I gave this problem to the Precalc Honors class, right before their lunch (the block is split into two parts). A couple of them came back with the solution, but most had chosen to eat and socialize (how dare they!). An epiphany hit me when I saw how a student had started to solve the problem. He added 1 + 2 + 3 + 4 + 5 + … + 11 + 12 to find out if the sum is divisible by 3 or 4.

My brain found the link to one of my very favorite math tricks / math stories: Little Gauss finding the sum of all the integers from 1 to 100.
So I put the following up on the board:

S = 1 + 2 + 3 + 4 + 5 + ... + 98 + 99 + 100. Find S.

Naturally a couple of the kids take the calculators out, so I go over and swipe the calculator out of their hands. I go through the whole story: An elementary teacher needed some quiet time to get stuff done, so the teacher asks the class to add all the integers between 1 and 100. Little Carl Gauss walks up in under a minute with the answer. Teacher is losing patience with this know-it-all, and asks him to add all the integers between 1 and 1000. Gauss strolls up in under a minute with the answer again. (Yes I dramatize the story. Sue me.)

So how’d he do it?

“You guys agree that I can write the numbers backwards and the sum will be the same right?”

S = 1 +   2 +   3 +   4 +  5 + ... + 98 + 99 + 100
S = 100 + 98 + 97  + 96 + 95 + ... +  3 +  2 +   1

What about if I add from top to bottom, what do I get?

2S = 101 + 101 + 101 + 101 + 101 ... + 101 + 101

How many 101’s is that?

2S = 101 x 100

…

S = 5,050

Go on to ask them what is the sum of all integers between 1 to 1,000 and find the following sum: 2 + 5 + 8 + 11 + … + 98 + 101.

Dividing Time Link

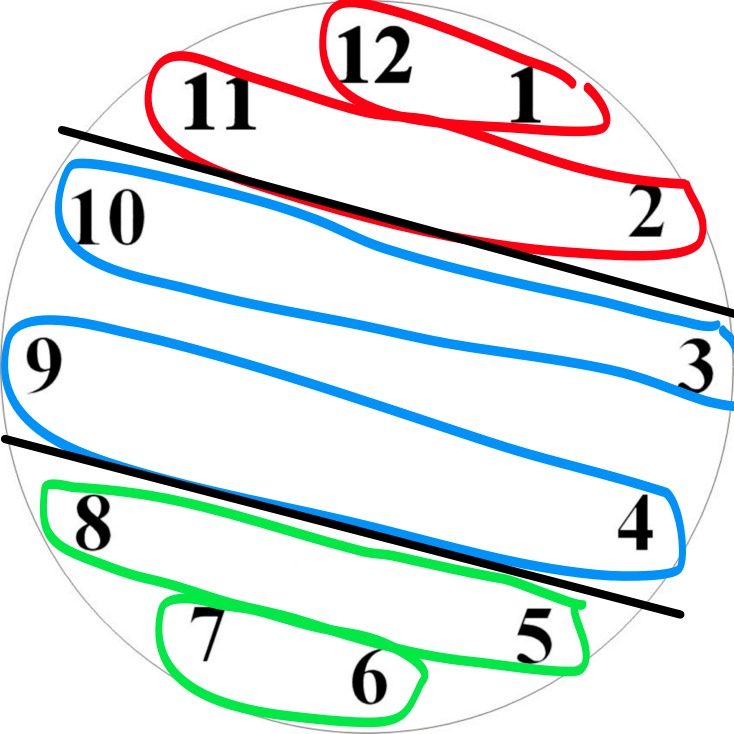
So back to the puzzler. Find the sum of the clock digits:

1 +   2 +  3 + 4 + 5 + 6 + 7 + 8 + 9 + 10 + 11 + 12  (then reverse them)
12 + 11 + 10 + 9 + 8 + 7 + 6 + 5 + 4 +  3 +  2 +  1

How many pairs (after you divide by the 2)? 
6 pairs.
So how many divisions of the clock by the two lines?
4 divisions wouldn’t work, so 3 divisions.
What are the divisions? Lets keep the pairs together so the sums are equal in each section.
Neat: