(This post demonstrates the math behind the creation of some unusual math art. I got the idea from this tumblr post which I don’t even think works like this. But it was the inspiration behind the pictures.)

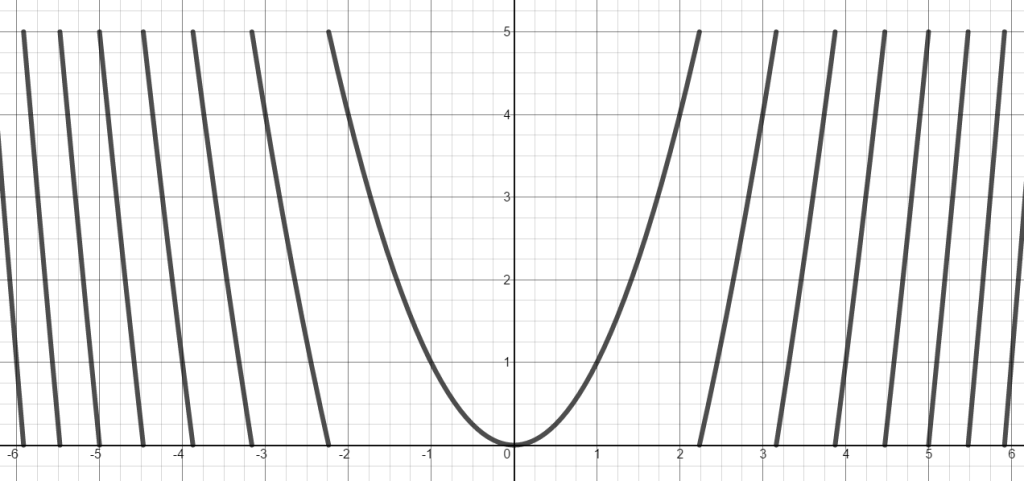
Take this function: f(x) = x^2 + a*cos(ax). When you take values of a between 0 and 8 and back to 0, you get the following:

I’d like to make an image that represents the entire family of this function. Problem one: the function values get pretty large in this window, so find the remainder of the function output after dividing by 5. Here’s the gif of that output:

Problem two: How do we represent this in one static picture? If you take the first image (where a = 0)

and take the function values from 0 to 5 and make the pixels for row 1 colored based on the function value (0 being black, and 5 being white), then you get this row of pixels (expanded to 20 pixels high for ease of viewing):

So this row of pixels represents a = 0. If you set a to be 0 at the top of the picture, a to be 8 at the middle of the picture, and a to be back to 0 at the bottom of the picture, stitch all these lines together you get:

Click on image for full 4k by 4k resolution.

Here’s another with the function y=(10a)/(1+x^2) with a going from 8 to 0 to 8.

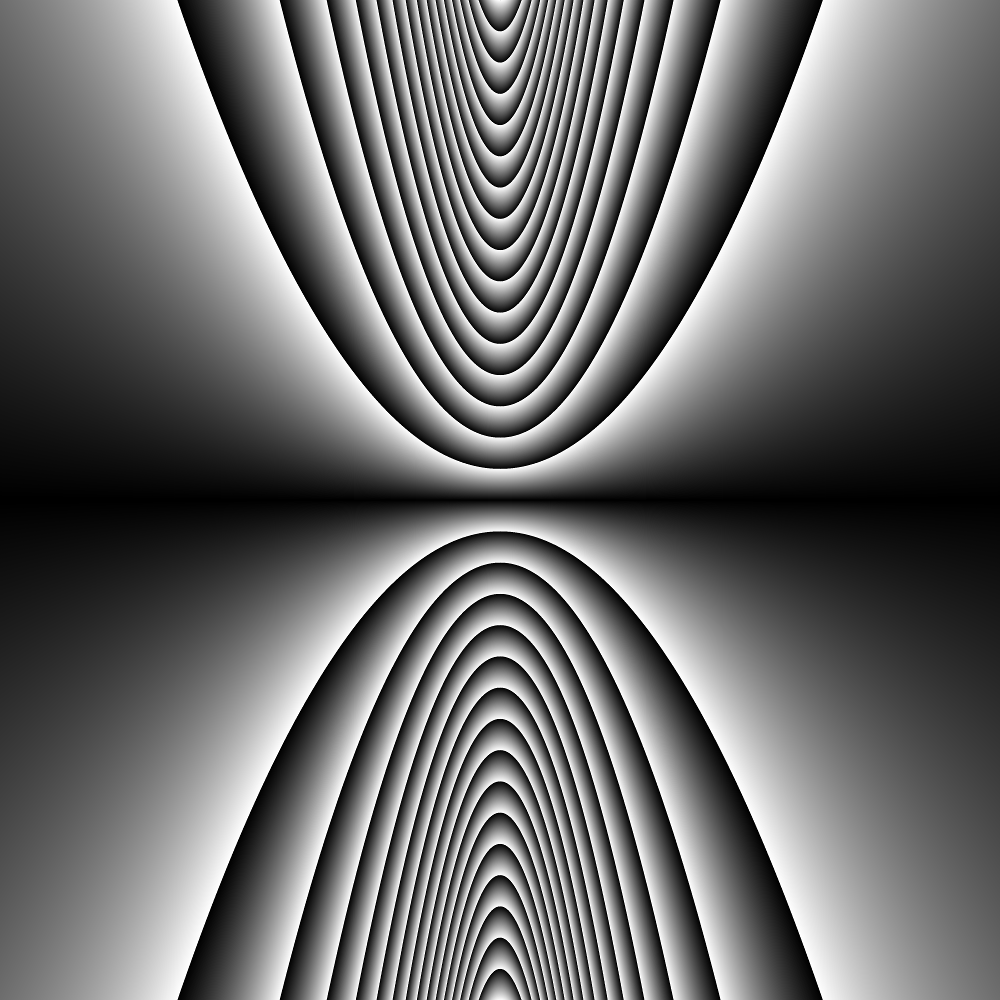
Click on image for full 4k by 4k resolution.

Here’s another with the function y=ceil(ax) – ax + floor(ax) with a going from 0 to 5 to 0.

Click on image for full 4k by 4k resolution.

And lastly, here’s the last one, but colorized. The 0 to 255 now controls the hue of the color (with full saturation and balance, using HSB color).

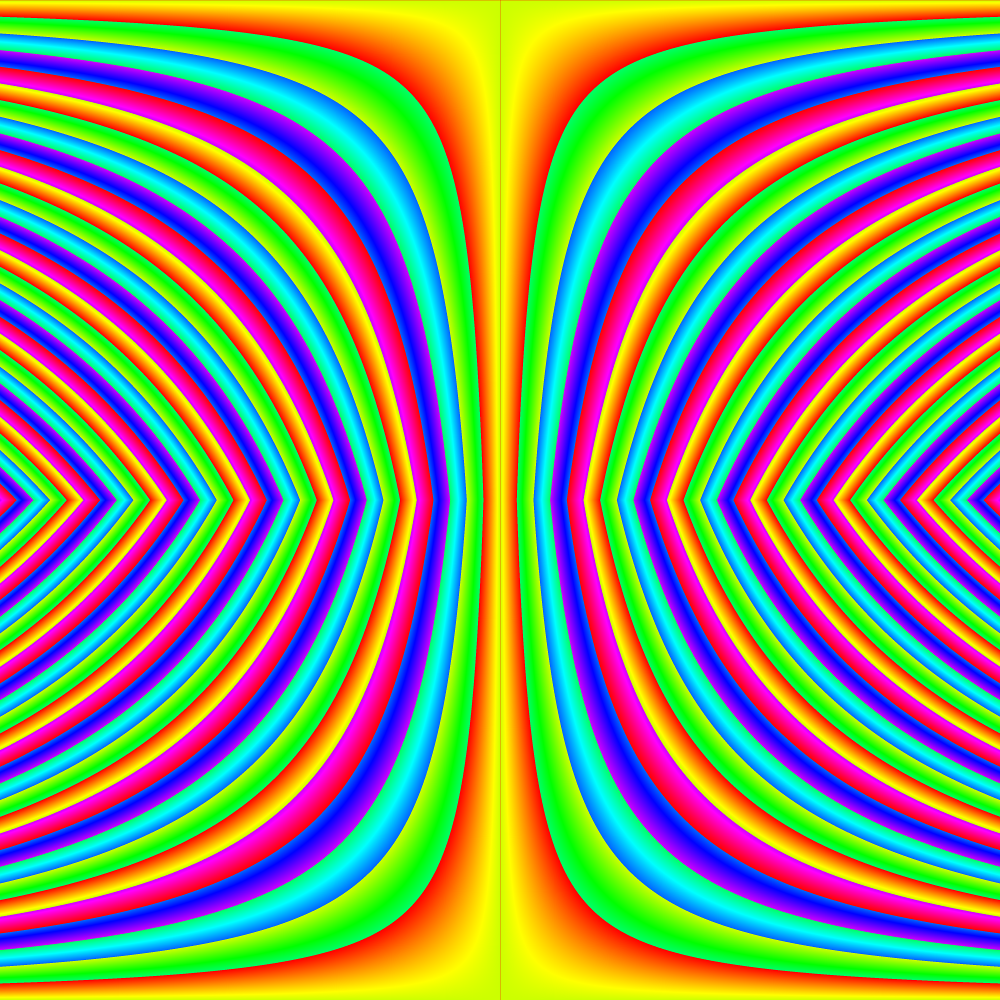
Click on image for full 4k by 4k resolution.

Here’s the code for those who are interested (or view it live on openprocessing)!

int max_a;

float mod(float a, float b)
{
  //desmos mod and processing mod act differently.
  //desmos mod always returns a positive value
  return (abs(a % b));
}

float func(float x, float a)
{
  //type 1
  max_a = 8;
  return (mod(x*x - a * cos(a*x),5));
  
  //type 2 this counts from a= 8 to 0 to 8
  //max_a = 8;
  //a = max_a - a;
  //return (mod((10*a)/(1+x*x) ,5));
  
  //type 3
  //max_a = 5;
  //return(mod(ceil(a*x)-a*x+floor(a*x) ,5));
}


void setup()
{
  size(1000,1000);
  colorMode(HSB,255);
  int w,h;
  float x,a,f,hue;
  max_a = 5;
  loadPixels();
  for (int i = 0; i < pixels.length; i++)
  {
    w = i % width;
    h = int(i / width);
    
    x = map(w,0,width,-6,6);
    
    if (h < height/2)
    {
      a = map(h,0,height/2,0,max_a);
    }
    else
    {
      a = map(h,height/2,height,max_a,0);
    }

    f = func(x,a);
    hue = map(f,0,5,0,255);
    
    pixels[i] = color(hue,255,255);
  }
  updatePixels();
  //save("type3c.png");
}

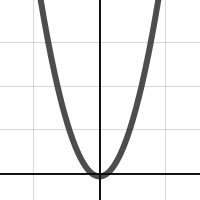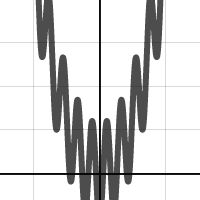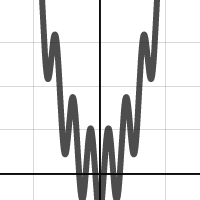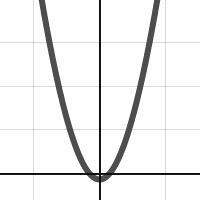
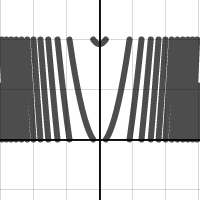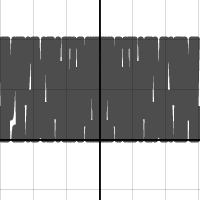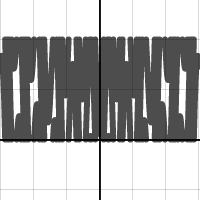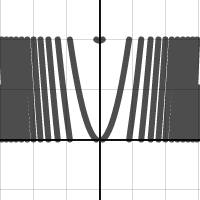
edit 10/16/15:
Here are a couple more pictures for you (the code on openprocessing is up to date with these new types):