It’s midterm week at school, and James Tanton threw out two interesting questions in two days. I spent a little time programming “solutions” to these problems (not solutions, just verifications for an infinitesimally small portion of the natural numbers).
Problem One:
Start with a prime, square it, and add 4. Repeat. (eg 3->13->173->…) Must eventually reach a non-prime?
— James Tanton (@jamestanton) January 27, 2014
Here’s my processing.org code for this problem. And here’s the output of the code, each time the sequence gets longer, it prints out the new “max” sequence length. 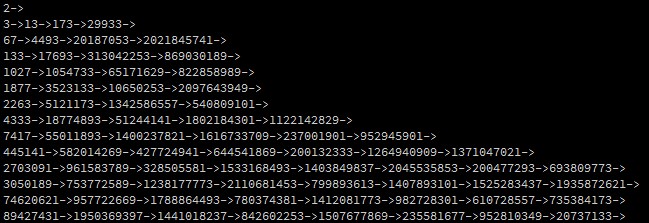
I didn’t use any of processing.org’s graphics but I had the prime function optimized, so it was quick work.
Problem Two:
Start with a whole number, square it, and add 4. Repeat. (eg 2->8->68->4628->…) Must every starting nmbr eventually hit a multiple of 13?
— James Tanton (@jamestanton) January 28, 2014
Here’s the python code for the “solution”. And here’s the last six lines of the output of the code.  I checked all numbers under 1,000,000, and all the sequences were finite (they stopped at a multiple of 13). The starting number whose sequence ended in the largest multiple of 13 was 964,665, and the multiple of 13 had 384 digits (BIG NUMBER! There are only ~10^80 particles in the entire universe). Fun stuff.
I checked all numbers under 1,000,000, and all the sequences were finite (they stopped at a multiple of 13). The starting number whose sequence ended in the largest multiple of 13 was 964,665, and the multiple of 13 had 384 digits (BIG NUMBER! There are only ~10^80 particles in the entire universe). Fun stuff.
[Edit: 1/28/2014 9:08am] Ok, ok. James asked for a proof for the second problem. Here you go 🙂 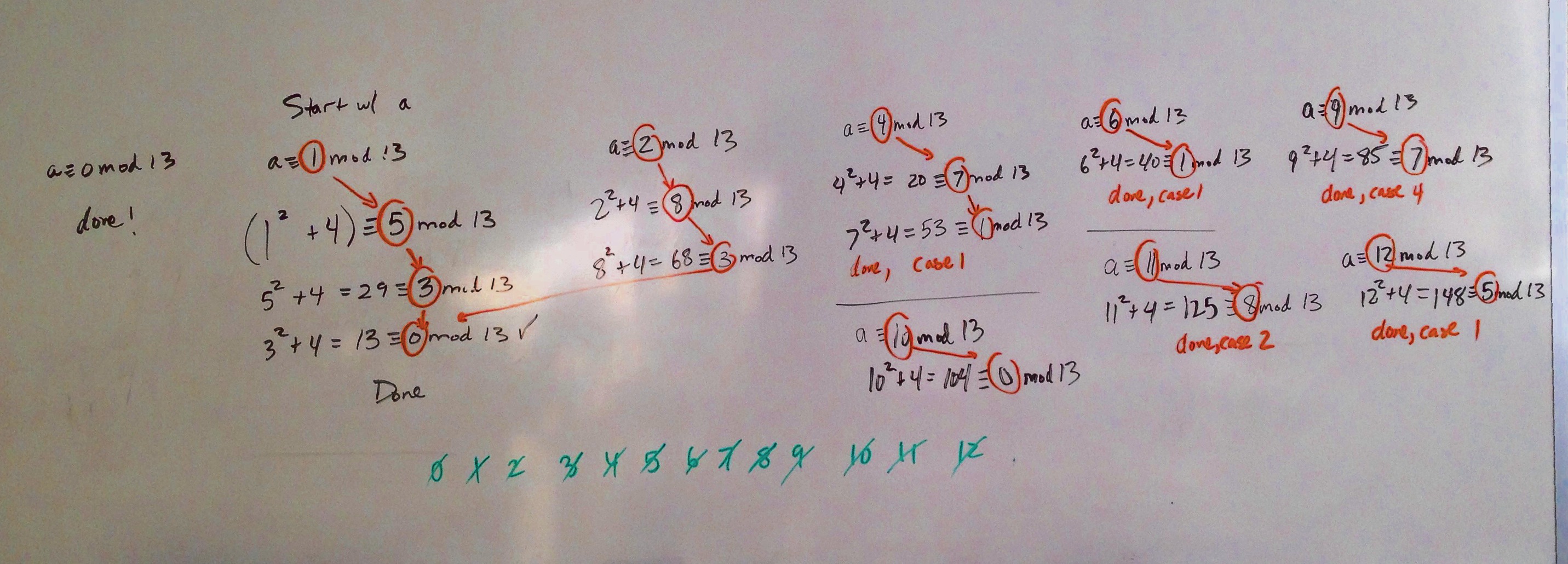

One Response to Two James Tanton Questions