Candle Burn #WCYDWT

by Dan Posted on May 23, 2011

The structure of this post comes from Dan Meyer’s Three Acts of A Mathematical Story.

Act 1

Play the teaser video.


Have students write down questions they have about the video. Ask them to be silent during this part so that other student’s questions don’t affect their own. By this point, I’m sure that 95% of them will have the same question: How long does it burn? Ask them to write down their guess to the answer to this question (once again silently). Record their guesses on the board; this tends to buy them into the process. There are reluctant guessers in every class who are afraid of being wrong and this is an important lesson for them to learn.

Act 2

Offer some resources for the students to work on.

All videos used the following stop-motion settings:
Two photos per minute.
Video compiled with 10 frames per second.

Small candle start mass: 13g
Small candle end mass: 5g

Medium candle start mass: 51g
Medium candle end mass: 5g

Large candle start mass: 287g
Large candle end mass: 30g

Using the stop-motion settings students first need to calculate how long the small and medium candles burned, in order to make a linear regression of candle burn mass vs. candle burn time.

Act 3

Answer video:

Have them calculate the final burn time of the large candle. Talk about possible error points (do color, fragrance, or other factors affect burn time?)

Maybe(?) show the following graph:

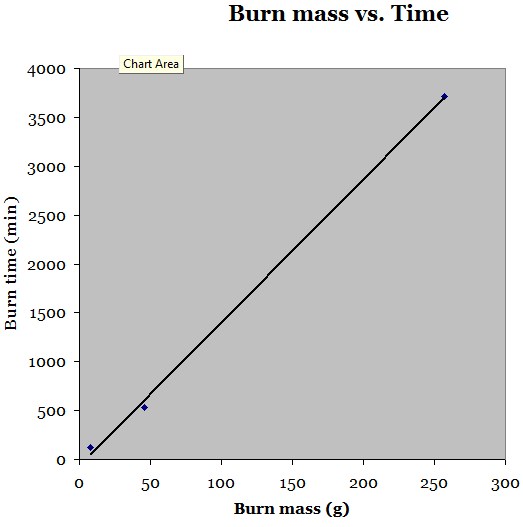
Extension Questions:

  • If I want a candle to burn for 100 hours, how large does it have to be?
  • If I have a candle with 3 wicks that has a mass of 150g, how long will it burn?
  • (more?)

As always any and all feedback is extremely appreciated by me. Please let me know what you think. I design this stuff in a vacuum and I want to know how to make it better. Thanks, Dan.

Posted in Full Posts | 12 Comments

Car Talk Puzzler (Palindrome Mileage)

by Dan Posted on May 23, 2011

New Math Puzzler up this week:

Tommy’s Drive to Work
RAY: Tommy has a new car, it’s 19 years old. … It has one of those newfangled six-digit odometers. It can register as many as 999,999 miles. 
So one fine morning last week, Tommy gets into his new car to drive to work. He fires up his engine and before pulling out of the driveway, he notices something interesting. His odometer reading is a palindrome. Do you know what a palindrome is?

TOM: No.

RAY: It’s a number that reads the same forwards as it does backwards. For example, if his odometer read 175,571 miles, that’s a palindrome number. 1 – 7 – 5, 5 – 7 -1, reads the same forward and backwards. ‘Well, that’s cool,’ he says to himself, and off he goes.

Naturally, he’s in no hurry to get to work, so he stops at his favorite café and gets his usual quadruple espresso macchiato, and about an hour later, he shows up at Car Talk Plaza. Just as he pulls into his ‘Reserved for the Big Cheese’ parking spot, he notices that his odometer reading again is a palindrome. And no, the odometer is not broken, but it is indeed a palindrome number once again.

So he’s gotten in the morning, seen a number, driven some number of miles – not many, cause he only drove for an hour,–not even, most of the time he was drinking coffee — and his new odometer reading is again a palindromic number.

Here’s the question: How far did he drive that morning?

I have a couple of answers with the same amount of miles, but it seems too low for driving for an hour. Even in a city.

Posted in interesting stuff | Tagged , | 4 Comments

Circle of Differences Puzzle

by Dan Posted on May 19, 2011

Great article from the NY Times on the Danger of Praise, with an excellent puzzle included:

Circle of Differences

The numbers 1, 2, 3 and 4 are written at the corners of a large square.  At each step, at the midpoint of each side, write the positive (or absolute value of the) difference between the numbers at its ends, so in the diagram below, you would write the numbers 1, 1, 1, and 3 at the midpoints of the sides, forming a new (tilted) square.

Joshua Zucker

Then repeat that process, writing the positive difference between the endpoints at the midpoint of each side. Eventually you will reach all zeros.

1. How many steps does it take to get to all zeros?

2. Can you increase the number of steps if you start with different numbers?

Inspired, I created a couple more shapes (triangle and hexagon) in Geometer’s Sketchpad, and quickly made a sheet up for my students, found here.

Do you see any interesting modifications to the questions? What are some solutions?

Posted in interesting stuff | Tagged | Leave a comment

Car Talk Puzzler: Math + English =

by Dan Posted on May 14, 2011

Car Talk has a new math puzzler up that mixes math and science:

There Was an Old Man…RAY: I’m going to recite an equation and, from that, you are going to give me a limerick that consists of five lines.
TOM: Does this limerick include Nantucket or the band at the Waldorf Astoria?
RAY: No! Here it is. The numerator is 12 plus 144 plus 20 plus 3 square roots of 4, divided by a denominator of 7. Then, that whole quantity is added to 5 times 11. Finally that whole thing on the left equals 9 squared plus zero.
Now, I’m going to give the last line of the limerick, and you have to come up with the other four lines. The last line is “is 9 squared and not a bit more.”

What is the limerick?

So the equation is: A limerick is:

Limericks consist of five anapaestic lines. Lines 1, 2, and 5 of Limericks have seven to ten syllables and rhyme with one another. Lines 3 and 4 of Limericks have five to seven syllables and also rhyme with each other.
(source)

And a couple of examples of limericks are:

‘Tis a favourite project of mine,
A new value of pi to assign.
I would fix it at 3,
For it’s simpler, you see,
Than 3 point 1 4 1 5 9

and a classic

There once was a man from Nantucket
Who kept all his gold in a bucket.
But his daughter, named Nan,
Ran away with a man
And as for the bucket, Nantucket.

(with more obscene varieties)

So what is the solution? A great problem to throw at the kids in your class who have strengths in subjects other than math.

Posted in interesting stuff | Tagged , | 6 Comments

Tech Trick: Quickly posting homework answers online

by Dan Posted on May 13, 2011

Here is a quick tech trick for quickly posting your homework key (or any document that doesn’t need to be editable). Because of my new homework policy, I’ve been posting my homework key on the classroom website on the day that I give the assignment out. This allows the students to check their answers (and work) at home.

I’m a big believer that if it isn’t easy and quick, it won’t happen regularly, so I had to find a way to streamline this process. Here it is:

  1. Complete the key with paper and pencil. I could technically do the key on the computer, but anything that requires even a little bit algebra is a nightmare to do with software. So the best hardware in this case is a pentel quicker clicker (0.5 mm for those asking, only a troglobite would use a 0.7 pencil).
  2. Take a picture of the key with Genius Scan+ on my iPhone. This software allows you to crop, convert to black and white (looks nice), and upload to dropbox.
  3. Upload image from iPhone to dropbox’s public folder.
  4. Go on computer to dropbox.com, copy public link for the picture.
  5. Paste link to public image on classroom website.

It seems like a somewhat complicated procedure, but steps 2-5 take about 2 minutes and this has been efficient enough to ensure that I’ve probably posted 90% of the homework keys buy cialis in China online. For me, that’s pretty good. If it’s not an easy enough process, then I won’t do it consistently.

Some kids have said that they do look online for the homework key and on the end of the year survey I’ll find out how many have used the classroom webpage to find the homework key.

Do any of you have any ideas on how to further streamline the process?

Posted in interesting stuff | Tagged , | 3 Comments

Link: Learning through Problem Solving

by Dan Posted on May 6, 2011

Great post from John Scammell walking through a how-to for “wcydwt” (what can you do with this) or “ltps” (learning through problem solving). Can we just call it great teaching?

Learning Through Problem Solving Process

1. Present the problem.

  • The problem is best presented using a multimedia artifact like an article, video, picture, story, song or any other multimedia artifact.
  • It is best if the question the teacher wants the students to explore is not explicitly stated in the artifact.

2. Have students come up with the question they want to answer.

  • Ask students what perplexes them in the artifact.  What questions do they have?  What do they wonder about?
  • Let this discussion go on long enough for them to come up with the question that you want them to answer.  This is the hook.  They feel like the question came from them, rather than their teacher.

…

Posted in interesting stuff | Tagged | 2 Comments

IcoSoKu

by Dan Posted on May 3, 2011

From the brilliant(?) minds at vat19.com, I present to you, the IcoSoKu:

Just thousands, that’s it?

In my list of mathematical strengths probability does not appear, but there are: 12 unique numbers (vertices of an icosahedron), so 12! = 479,001,600 ways to arrange them. But because of the symmetry involved in a icosahedron, there are 12 ways to arrange a single icosahedron. So 12! / 12 = 11! = 39,916,800 ways to arrange the vertices. If each setup of vertices only has one solution, then that’s it, but I’m not sure if each solution is unique. If each tile is unique, then there are 20! ways to arrange the tiles, but I don’t think that comes into play for the number of challenges.

Am I missing anything? Is this interesting? Keep delving?

Anyway, interesting use of Platonic solids. BTW, bought it and it’s in the mail.

Posted in Full Posts | Tagged , | 7 Comments

Link: SBG… Why?

by Dan Posted on May 3, 2011

Great post from Terie Engelbrecht:

1) I do it so students can focus on learning, not points or effort.
2) I do it for students who take longer to make their own meaning; those same students that often get plowed under in the points-chasing game school often is.
3) I do it for students who may be considered “slackers,” but who still deserve a fair shot at showing me evidence of understanding. (And often times, those are the students that do understand it, without having to do a lot of “busy work” outside of class.)
4) I do it so students can reach true understanding, because I believe every student has the ability to do this.
5) I do it so students considered “high-achieving” can refocus on the true purpose of school.
6) I do it so students can stop categorizing and judging each other according to the letters A, B, C, D, and F.

I do it for students.

Posted in interesting stuff | Tagged | Leave a comment

Car Talk Puzzler: In Search for Bogus Coins

by Dan Posted on April 28, 2011

In Search of the Bogus Coins
RAY: We have seven stacks of coins, each with 100 coins. Real coins weigh ten grams, and phony coins weigh 11 grams. We’re going to weigh the coins on an analytic scale, which works just like your average bathroom scale – but it’s accurate to within a tenth of a gram.

Here’s the rub. Unlike our many fine previous coin puzzlers, in which you have one stack of coins that’s counterfeit, this time you could have several stacks of coins that are counterfeit.

TOM: If one coin in the stack is counterfeit, they’re all counterfeit?

RAY: Yes. But, it could be that none, some or all of the stacks of coins are bogus. You don’t know.

The question is, what’s the fewest number of weighings you need to make, to determine which of the stacks, if any, has counterfeit coins?

TOM: And how come it’s only one weighing?

RAY: Okay, wise guy. That’s right. That’s part two of the puzzler. How come it’s only one weighing – and how are you going to do it?

This is cartalk’s puzzler for this week (April 23rd through April 30th, 2011). If you answer on their website, you could be chosen to win a prize!

Hint: Power of binary numbers.

Posted in interesting stuff | Tagged , | Leave a comment