(note: this post was previously under: Two problems, but it seemed better to split the two problems into separate posts. The other problem is found here.)

How many people where at the Rally to Restore Sanity and/or Fear?

Gave the applied math class this picture:

(thanks to @samjshah for finding this image for me.)

Asked for, and recorded guesses.  The guesses weren’t half bad because many of them tried to compare the crowd to concerts that they’ve been to.

Asked them what information they needed to find the size of the crowd.

• They asked for the size of the crowd.  I played dumb, and asked them what they meant, they said the area that the crowd took up.  We used mapmyride.com to find the approximate dimensions of a rectangle holding the crowd.
• They asked how much space a person takes up.  I googled it, got this which says that the 2006 international building code says “5 square feet & 7 square feet if the person is dancing.”  Asked them if that made sense.  THANKFULLY our school has tiled the classrooms with 1 square ft tiles, so they all looked at the floor, many of them stood up, and held their arms out.  There was some disagreement, but the consensus was 6 square feet.
• Proportions to the rescue again!  And our answer was about 260,000 in the first class and 225,000 in the second class.  I didn’t guide their hand at all in these estimates, they controlled all the variables, and yet our results are on par with CBS estimate of 215,000. They liked the idea that their estimate was so close to the “official” estimates, and yet it only took 30 minutes to calculate.

(addition: Interesting article on the difficulties of counting people in a crowd: http://www.bbc.co.uk/news/magazine-12879582)

(note: this post was previously under: Two problems, but it seemed better to split the two problems into separate posts. The other problem is found here.)

If you could, how many folds of a sheet of paper would it take for the thickness of the paper to reach the moon?

Asked for them to write their guesses down first. They are so damned hesitant in math that this takes numerous trips around the room to get them all to record an independent guess. This is a class of kids who have failed often in math, so the fear is evident in their eyes. Next I write their guesses on the board, most of the guesses are in the hundred’s of thousands to millions range.

I asked “What information do you need?”.

• They asked for the distance to the moon; wolframalpha’ed (yes, I just verbed it) it and gave it to them in meters.
• They asked for the thickness of paper, so I gave a couple students a sheet of paper and a caliper. They tried to find the thickness, and then rolled their eyes at me, so I asked what do you want? They said more paper, so I gave them a ream of paper (500 sheets), and they found the thickness.
• To keep everyone on the train, I gave them a skeleton setup for how to find the result (e.g. How many layers of paper with one fold, two folds, three folds, etc).
• (semi-furious calculations commence. Many of them are finding out that the calculator on their smartphone is not so smart, so they ask to use each other’s calculators. Maybe 4 kids actually end up bringing their calculator to class, sigh.)
• Answer found is the same as in the video that spawned this investigation: found here.

My first favorite part about this calculation is that I was able to show them how quickly a spreadsheet calculates the same result after they’ve filled a sheet of paper with numbers. They had use of the laptops if they wanted, maybe this will help buy them into the usefulness of spreadsheets. Maybe not.

Me second favorite part about this calculation is that they’ve all tried to fold a sheet of paper as many as times possible, and many of them have seen the mythbusters episode with the folding paper. It’s a problem whose result shocks them, and I like that.

The second class of students that I gave this to, had 3 kids who had already seen the video with the answer, and the magic was significantly reduced for order cialis canadian pharmacy the whole class because they knew that someone else already had the answer. Much less driven to find the answer. Lesson for me: Verification isn’t anywhere near as exciting as Mystery.

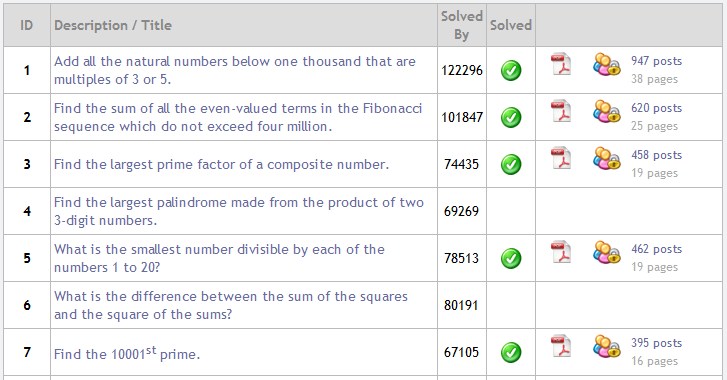
This is the second time I’ve done this lesson.  You can read up on the previous attempt here.

Quick synopsis: There is a local contest to determine how much a large pumpkin weighs, the winner receives a year Family subscription to the YMCA (worth about $800).  This contest concludes on Halloween.

Step 1: Find the dimensions of the pumpkins.

Here is the pictures I gave the Applied Math class:

Much thanks to Lisa Henry (@Mrs_LHenry) for the pictures.  I asked; she delivered!

So the class was able to find dimensions of each of the measurable pumpkins using proportions^[1] and scale factors based on the business card in the picture.  Next I gave them pictures of the pumpkin that we wanted to find the weight of:

FYI, the size of a pack of Extra Gum is: 6.2cm by 7.7cm.  Finding the dimensions was step 1.

Step 2: Graph Scatter Plots

Next the students had to graph a scatter plot of the dimensions to see if there was a corrilation between the dimension and the pumpkin weight.  The three graphs they had to create were: height vs. weight, length vs. weight, and cross-sectional area vs. weight.  It turns out that our data didn’t show any correlation between the length of the pumpkin and its size.  Good (not great) discussions followed, talking about how life doesn’t always work out like you wish it would, and how data doesn’t always fit our hypothesis.

Also it seems like one of the pictures was significantly off when compared to the others.  The pumpkin above with the weight 1208 pounds appears to be much more dense compared to the other two pumpkins.  It was an outlier for our graphs, and this led to some important discussions as well.

Step 3: Put your money where your mouth is

The students all got an entry form to fill out, and they had to put their calculated guess on the whiteboard.  The following are their guesses:

Step 4: And now for the horribly disappointing answer

632 pounds.

Ok, so we were waaaaay off.  Nearly by a factor of two.  I think I may know the problem, and it is possibly math related.  I’ll give you some time to think about it.

.

.

.

.

.

.

.

.

(Rhode Island is neither a road, nor an island.  Discuss.)

.

.

.

.

.

.

.

.

I think the problem lies in difference of how the photos were taken of the pumpkins.  Notice that in the pumpkins that we know the weight of, the business card is in front of the pumpkin, and in my photo of the Riggi pumpkin, the pack of gum is on-top of the pumpkin?  

Since the pack of gum is on top of the pumpkin in my picture, if it was in front of the pumpkin like in the other pictures, it would appear larger, and the Riggi pumpkin would appear smaller.  Making the calculated weight of the Riggi pumpkin go down.  Sigh.  Maybe next year.

____________________________________________________________________

I think that if the students learn one thing in math class, proportions should be it. There is nothing more useful in everyday life then a good proportion.Back to Post