I saw this fantastic webpage a couple of months back.
Tons of fun. I took that idea and made a gif for my weird art Tumblr, Recursive Processing.
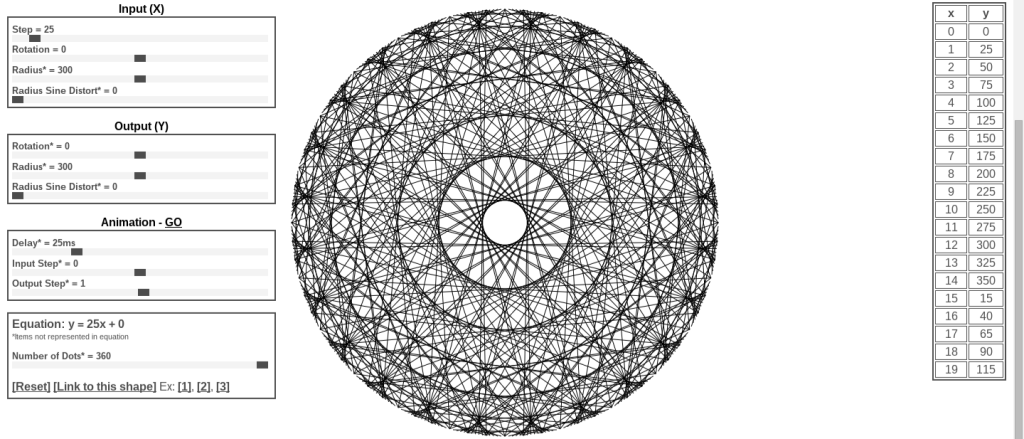
Here’s the processing.org code and the live (and smoother) version, and here’s the more fun version that is interactive based on the mouse position (some interesting polar math is involved here, x = r cos (theta) and y = r sin (theta) ).
These all work on the same principle, take a bunch of points around a circle, and shift them around the circle based on a linear function. If the output is too large, then they wrap around (clock math). The formal name for this idea is modular arithmetic, a very useful concept in computer programming. A quick example: Take an input value of x = 120, and a function of y = 3x + 20 (mod 360). y = 3 (120) + 20 (mod 360) = 380 (mod 360) = 20 (the remainder after dividing by 360). So make a line between 120 on the circle and 20. The resulting image after calculating 360 different points for y = 3x + 20 is:
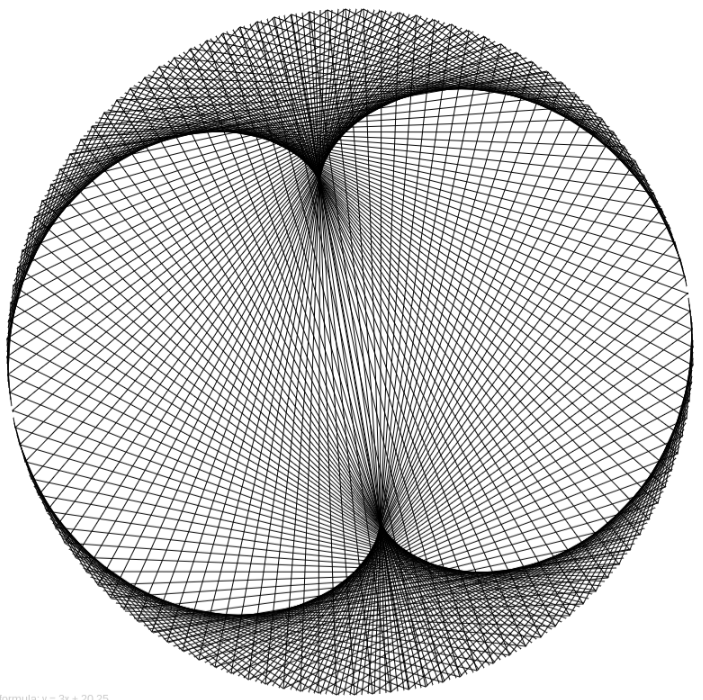
But this concept is more difficult to grasp with the unusual step of graphing the points around a circle.
Separate Input from Output
Lets go to a more straightforward representation. Here’s an interactive that might help.
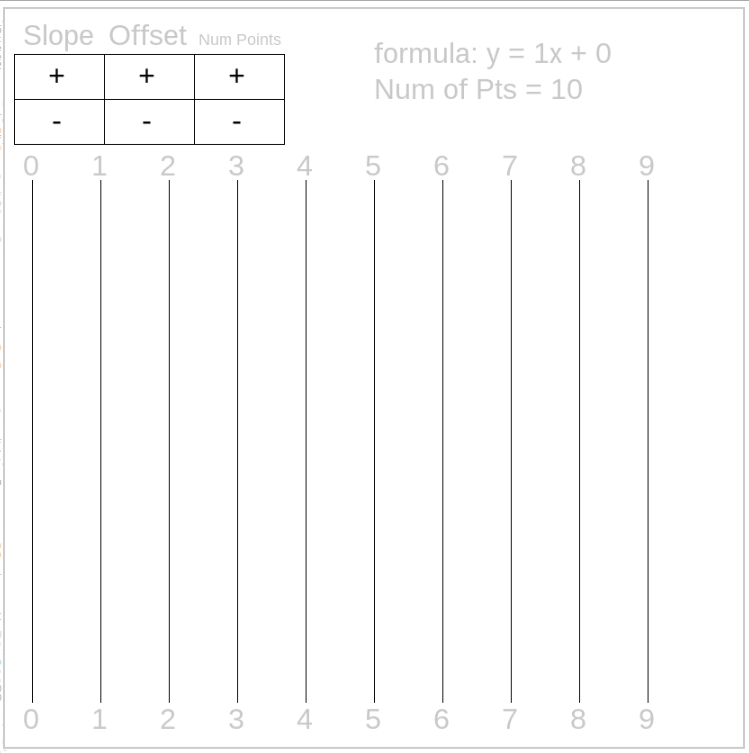
So, this is just about the least interesting function, y = x (mod 10). So if x = 3, then y = 3 + 0 (mod 10) = 3. So draw a line from 3 to 3. Try the interactive yourself, click to change the function and see how it changes the picture.
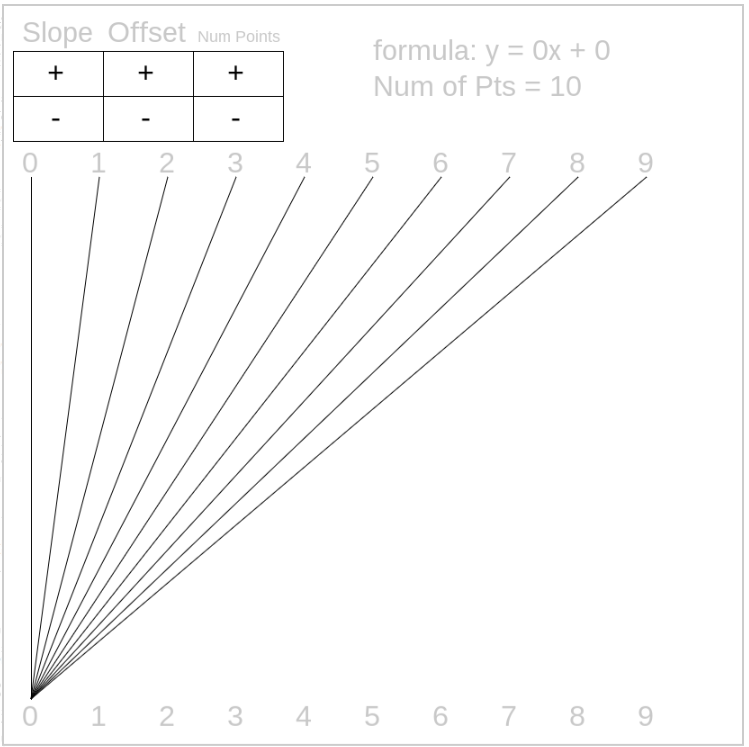
Here’s another boring function: y = 0x + 0 (mod 10).
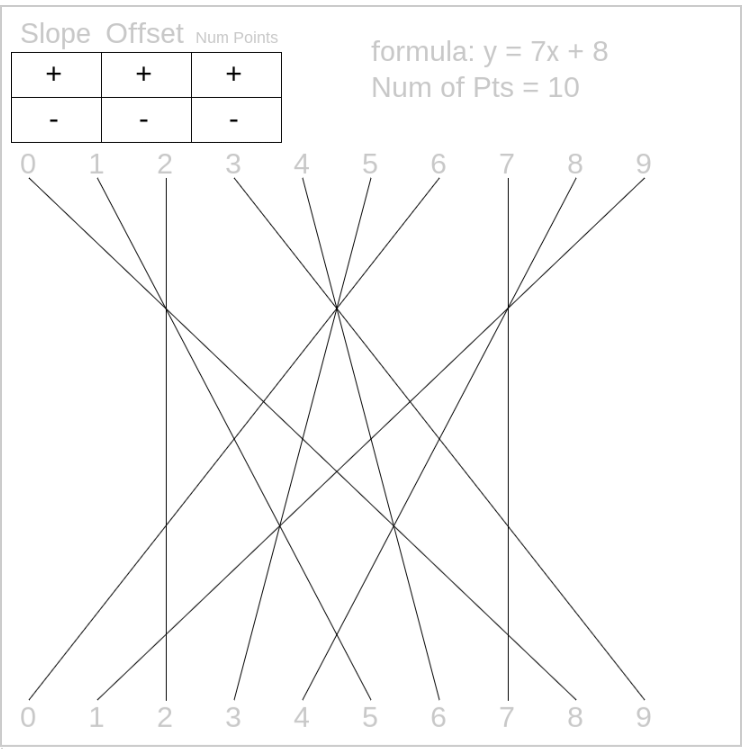
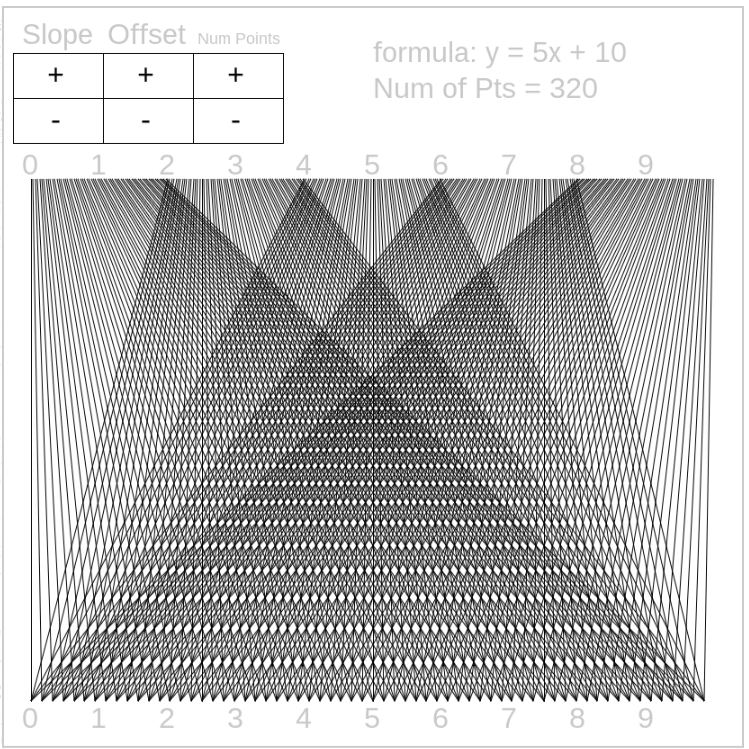
Ok, lets get to the interesting stuff, y = 7x + 8 (mod 10). Take x = 4, so y = 28 + 8 (mod 10) = 36 (mod 10) = 6. Draw a line from 4 to 6.
Here’s another interesting picture:
If you really enjoy the picture that you’ve made then you can get a high definition version (5k by 5k) by copying the code, installing processing.org and clicking any key. The image will be in the same file as project. Very good for printing in large form if you’re lucky enough to have a big printer.
New artwork in the classroom today. Told you I'd be dangerous when I figured out how to use the plotter. pic.twitter.com/479YZnWNdy
— Dan Anderson (@dandersod) April 24, 2015
Questions For You
How can I bring this into the math classroom?
Where does this fit?
Is modular arithmetic in anyone’s curriculum? If not, why not?
Should I (or you) put together a non-linear version? Exponential, powers, logarithmic?
Other thoughts?


4 Responses to Linear Modulus Art
Pingback: Tracking Venus and Earth over 8 years | A Recursive Process
Pingback: Sample Post: Tracking Venus and Earth over 8 years | Math Projects