I’ve given this presentation in November 2014 at AMTNYS in Syracuse, and in April 2015 at NCTM in Boston. I’ll be giving the presentation in May 2015 at the NY Master Teacher Conference, and in July 2015 at Twitter Math Camp in Claremont CA. 

Drive

Why use the Mandelbrot fractal to get the students to learn some Precalculus topics?

• How often do students study math that less than 40 years old? Think about it.
  What’s the most recently developed math topic that happens in your classroom? The Mandelbrot fractal was developed (discovered?) in the late 1970’s by Benoit Mandelbrot (amongst others, more information here) while working at IBM and through working with the Julia sets. His collegues at SUNY Stony Brook* used computers to create the first image of the Mandelbrot Set:
  
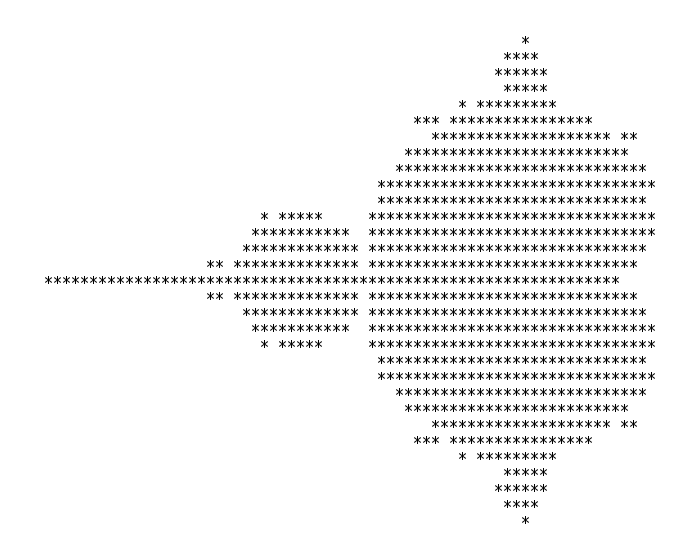
  The first picture of the Mandelbrot set, by Robert W. Brooks and Peter Matelski in 1978/1979*.
• There are so many great Precalculus topics addressed by the Mandelbrot set, namely:
  • Complex numbers
  • Arithmetic with Complex numbers
  • Complex plane and Argand diagrams
  • Recursive sequences
  • Polar Form of Complex numbers
  • Graphing using the Polar plane
  • DeMoivre’s Theorem

  By themselves they are interesting topics with many diverse uses, but together they can do marvelous things.

• The utter beauty and mysterious nature of the Mandelbrot set (and other related sets). It seems so inapproachable. Scary. It’s an infinite complex process and has all the crazy fractal properties of self-similarity, but not really. You can zoom in forever and get more and more detail as you go. You can create (and understand?) images like so (all of these images came from my amateur code).
  
  
  
  
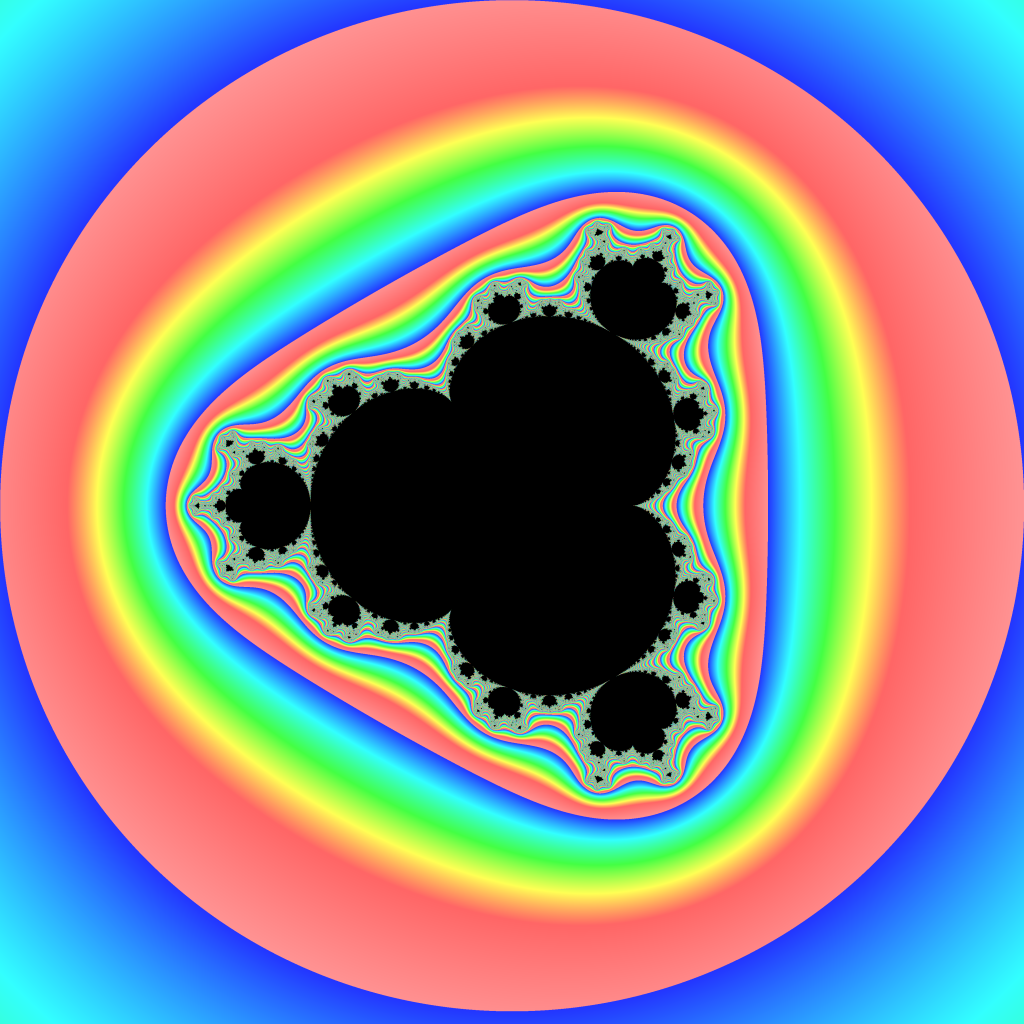
  But these images are only finitely interesting. They are just pixel representations of the actual fractal. We can zoom in and get as much detail as we can handle (or more correctly, as a 32bit processing.org decimal float can handle – duh).
• Lastly, be selfish, wouldn’t you like to learn something new alongside your students? Isn’t trying new things inherently a sign of youth? This might not be your thing, but if you’re interested in bringing it back to the classroom, the students will be that much more interested to see the teacher learning alongside their students.

How

Here are several good videos that can help you get started with the Mandelbrot set:

• The Mandelbrot Set from Numberphile and Dr Holly Krieger from MIT.
• 63 and -7/4 are special from Numberphile with Dr Holly Krieger from MIT.
• Mandelbrot Set: how it is generated.
• How to fold a Julia Fractal. Amazing website.
• And for fun, music video for Jonathan Coulton’s song Mandelbrot Set

Next, you can walk through the lesson outline that I’ve made (pdf) and through the presentation that I gave for NCTM Boston (pdf).

Here are links to all the interactives:

• Clicker
• Mandelblocks
• Mandelbrot
• MandelbrotZoom
• MandelbrotFamily
• JuliaZoom
• MandelbrotAndJulia
• MandelbrotExperimental

Everything is also found here: bit.ly/mandelbrotfractal, including all the presentation material, the walkthrough, the interactives (and all the source code).

I had a ton of fun with this project and presentation, and I hope the students did too. Please let me know if you have any questions or comments. Thanks!

*Errors fixed thanks to a comment by J. Peter Matelski (one of the original Mandelbrot developers!)